Posted on

Analyzing Polynomial Graphs

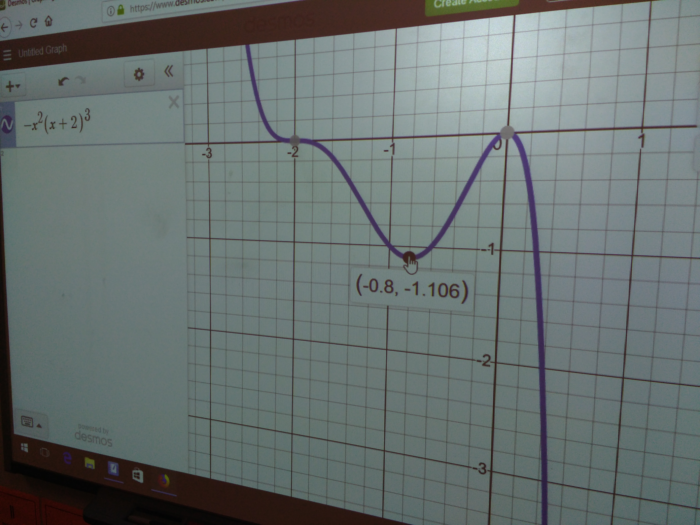
Here’s an INB page I created to introduce students to analyzing graphs of polynomials.

Each graph is repeated three times, so we can (literally) highlight different aspects of it. Luckily for me, Sarah is amazing at acquiring classroom supplies, so I have a lot of highlighters for students to use.

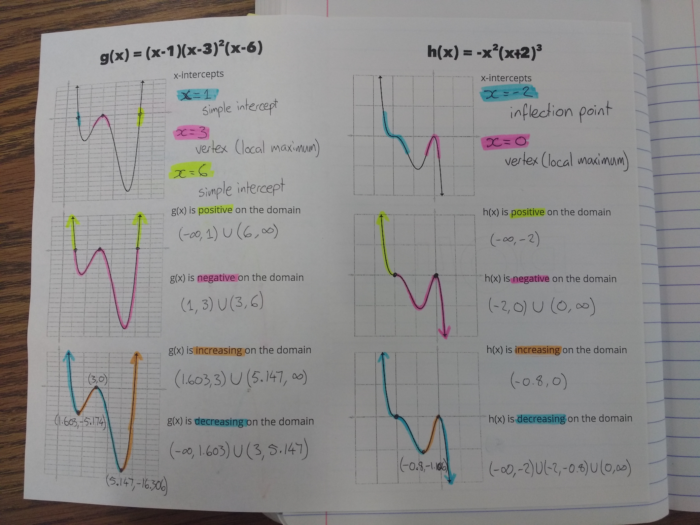
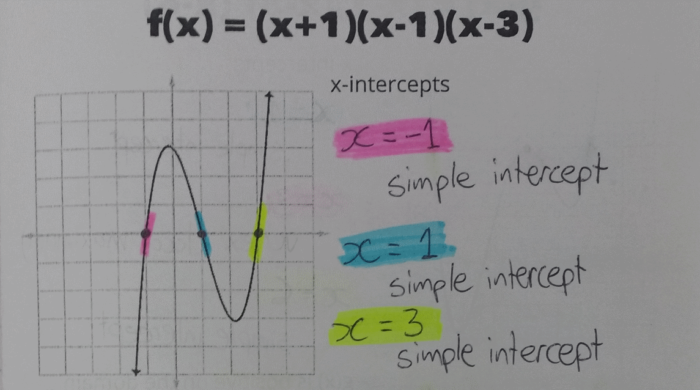
The first part was identifying the x-intercepts and the nature of each of the intercepts. I had students highlight the curve around each intercept, to emphasize whether they are simple intercepts, vertices (local minima or maxima) or inflection points.

As students did this, I tried to direct the conversation to figuring out why particular polynomials led to particular types of intercepts. This was actually really easy, as the class were asking and answering these questions without much prompting from me at all.

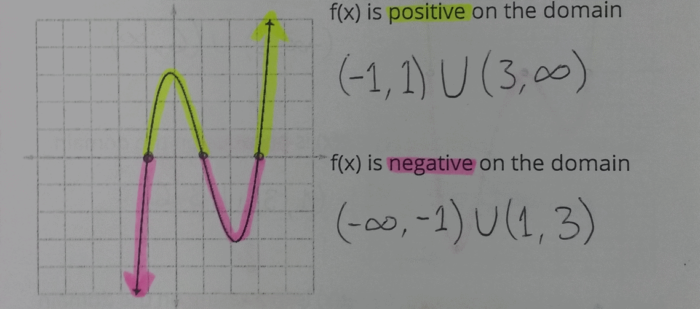
Next, we found the intervals for which each polynomial is positive, and for which they are negative. Having students visually represent the sections which are positive and negative really helped them in identifying those intervals.

I just (as in, while I’m writing this post) had an additional  idea to help with this part. If I’d given each student a card, they could place the edge of it along the x-axis so that only the positive parts of the graph were showing. They’d highlight those parts of the curve, then flip it over so they could highlight the negative parts of the curve.

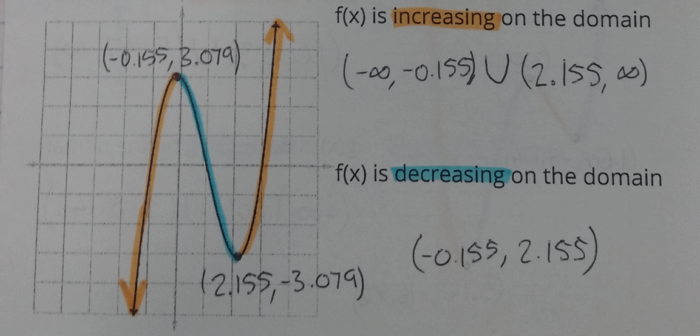
Finally, they highlighted the sections which were increasing, and the sections which were decreasing. To find each local maximum and minimum, I just had to quickly teach them some differential calculus…

… just kidding. We used Desmos.

Joking aside, I do like using topics like this to start hinting at the math that students may be seeing in the future. I was able to explain that a big part of calculus is looking at the rate and direction of functions, with a particular focus on where functions are neither increasing or decreasing.

If you’d like these notes, downloads are available here.

I used https://www.graphfree.com/ to make the graphs. I know I’ve made my own graph sketching tool before, but it’s really only capable of parent functions and simple transformations of them, so GraphFree was exactly the tool I needed this time. (To be honest, the main reason I’m mentioning GraphFree here is I’d forgotten what GraphFree is called when trying to find GraphFree the other day, so I want to remember that GraphFree is called GraphFree. GraphFree.)

Following this, we did further practice using section 6.4 of the practice book I’m working on. Follow that link if you’d like to get those practice questions yourself – for free!

 
Posted on

Algebra 2 Practice Book ver 0.1.1

Here’s the latest version of my Algebra 2 Practice Book. I’ve started Chapter 7 now, with questions for the following sections:

7.1 Reciprocal Functions. I prefer this title over “Inverse Variation”, as that’s too easy to confuse with inverse functions.

7.4 Simplifying Rational Expressions. This also includes simplifying products and quotients of rational expressions

Downloads are available here:

Mr. Carter’s Algebra 2 Practice Book
Version 0.1.1 (January 30, 2018)

Chapter 5: Polynomials Part A

Chapter 6: Polynomials Part B

Chapter 7: Rational Functions and Expressions

A reminder that these are early drafts of what is very much a work in progress. All content is subject to change.

Copyright Shaun Carter © 2018. Teachers may reproduce these documents for use in their own classroom only.

 
Posted on

TI-84 Guides for Univariate and Bivariate Statistics

Here are some guides I made for my students to help them remember how to use the TI-84 Plus CE (though I think it’s pretty much the same for all TI-84s) to calculate statistics and create graphs for univariate and bivariate data. They’re designed for interactive notebooks, but I’m sure they’d still be useful for teachers who don’t use INBs.

1-Var Page 1: Entering Data and Calculating Statistics

1-Var Page 2: Histograms

1-Var Page 3: Boxplots

2-Var Page 1: Entering Data and Calculating

2-Var Page 2: Scatterplots

2-Var Page 3: Regression

Downloads are here.

 
Posted on

Perimeters of Polygons INB Page

I mentioned in my last post that students sometimes describe perimeter as the “outside of a shape” (as opposed to area being the “inside”.) Though it’s an easy answer to give, and an easy answer for a teacher to accept as being correct, I wanted to put my students’ understanding of perimeter on a more sure footing. I wanted to give students a clear definition, showing that when we use the perimeter, we’re talking about a length.

At the same time, the math involved in the perimeter of polygons is pretty simple: its the sum of the lengths of the sides. There’s a reason it’s introduced at third grade (in the Oklahoma standards, at least.) But while adding a set of numbers is pretty easy for a high school student, I wanted to layer in more challenge.

My students need to figure out the missing side lengths of the polygon before they can make that simple calculation. Or, they’ll get the perimeter and have to figure out something else. Given this unit has already covered theorems related to quadrilaterals, and the previous unit was on the Pythagorean theorem, special right triangles and trigonometry, I had lots of options of for how to make students determine the information they need.

Also, students complain all the time about word problems, which tells me they probably need more exposure to and practice with word problems. So I gave my students ten problems, for which they had to draw a diagram (as I hadn’t given them one) and show all their mathematical working.

Downloads are available here.

 
Posted on

Areas of Polygons Cut and Paste Activity

One of the biggest challenges in teaching math is allowing students to understand things that are abstract. For instance consider this possible definition for area: “A measure of the two-dimensional space within or occupied by a plane figure or region.” While this seem perfectly serviceable to a math teacher, students may struggle to conceptualize exactly what it means. What exactly does two-dimensional space mean? What does it mean to be “within” a figure or to “occupy” space?

These seem simple, but there are subtleties to understanding what area really is, which I’ve even seen calculus students mess up with. If you ask students what area is, they often respond with something like “area is the inside, and perimeter is the outside,” but then can’t elaborate on that. The common confusion between concepts of length and area is demonstrated by students frequently stating the area of a shape in length units.

This is why I like using the cutting and pasting of paper to represent area. I find students can conceptualize the amount of paper used to make a shape much easier than the abstract idea of “area”, even though they are fundamentally the same thing. Students can understand that one shape has more area than another using the fact that it took more paper to make. Also, if you can demonstrate that two shapes can be constructed from the exact same amount of paper, students can understand that they have equivalent areas.

This activity uses the area of a rectangle to find the areas of other polygons. Students are given a page with templates for the shapes they’re going to create, and a colored half sheet of rectangles and octagons. (The colored half sheet is actually double the number of shapes they need, but it makes things easier to have spares if they make mistakes.)

Everyone also needs a glue stick, a pair of scissors, a ruler and a pencil.

The white sheet can be cut into the six separate sections. On the back of each section, there are instructions on how to construct the given shape from a rectangle.

Students should follow the instructions to construct each shape from one of the small colored rectangles. Reactions will range from “this is easy”, to “I think I’ve got it, can I check what you did”, to “this is impossible!” Make sure you’re cycling around the room a lot, because students can and will fall behind quickly if they’re not paying attention. Frustratingly, I found most of the students who thought the instructions didn’t make sense hadn’t actually taken the time to read them step-by-step.

I suggest doing them in the order of rectangle, parallelogram, triangle, trapezoid, kite and polygon. Once they’re done, they’ll look something like this:

The idea is that each shape has an area equivalent to a rectangle in some way, because they used the same amount of paper. The triangle and the kite are related by a half, because one rectangle was able to make two of these shapes. The regular polygon is a little different, as it starts with the polygon and is deconstructed into half a rectangle; we know it’s half, as we already showed that triangles make the area a half. Add some labels to the shapes, and you get something like this:

In the trapezoid, “m” is referring to the midsegment (or median) of the trapezoid. We’ve already covered the the theorem that says the midsegment length is the mean of the base length, which is why we’re able to substitute (b1 + b2)/2 for m without any further working.

If you’d like to do this, files can be downloaded here. Included are alternate versions for non-Americans who think “trapezoid” is a weird word. Font is Matiz.