Problem I gave to Year 9 a few weeks back: Imagine taking an A4 sheet of paper, and cutting the corners out so it folds into a box. What is the maximum volume possible?
Or how I actually presented the problem:

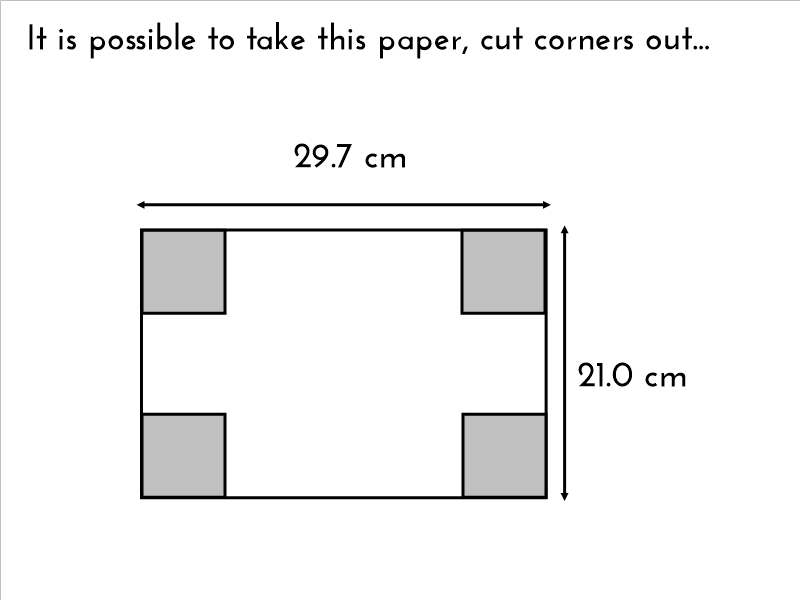
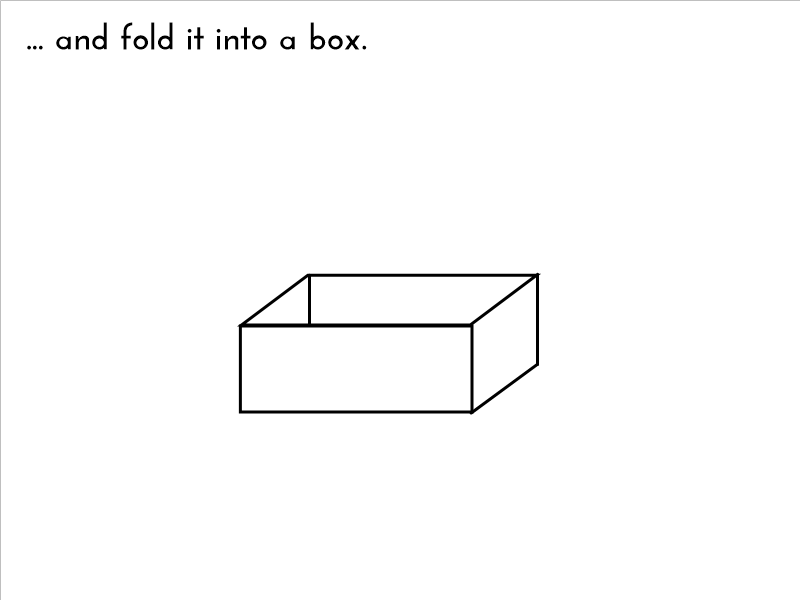

I’m sure that any non-metric types could easily adapt this to letter size paper. 😉
This is the type of question I’d typically use with my Year 12 class, and expect them to use calculus to solve. But Year 9 had to use other strategies. (One student did manage to find a website that told him he would have to use differentiation, and wanted me to teach him what it is, there on the spot…)
So, trial-and-error was the game instead. Some students realised this immediately, while others needed a little bit more of a push. I remember being a student and hating trial-and-error as a strategy, because it always seemed to me that there should be a more efficient method to solving each problem. Of course, there usually was.
I’m realising more that giving students a task that’s relatively easy, but also slightly tedious, is a great way to provoke curiosity with the question Is there a better way to do this? Of course, I always prefer it if the kids are asking, and answering, that question themselves.
The reasoning that students went through went something like this:
- I’ll just pick a size for the corner, and see what that is. (Some of them found it a little difficult to reach this by themselves, so I had to suggest it.)
- Now I can find the dimensions of the box.
- Now I can find the volume.
- I should try this with another size corner.
- Huh, that made it bigger/smaller.
- This is taking a while, maybe there’s a pattern to calculating these.
- Even with a pattern, this is still taking forever.
The next step, which I had to hint at a bit for them to get it, was that they could use their computers to do the repetitive work for them. Because of my well established obsession with Desmos, they quickly guessed that Desmos could be used. So they started doing something like this:
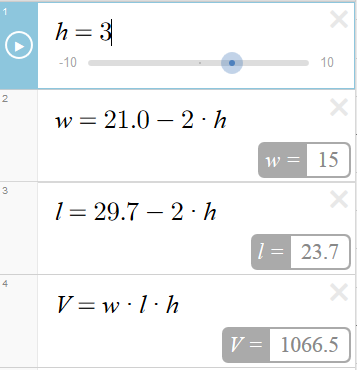
I think this type of frustration, where a problem is easy but tedious and crying out for a more elegant solution, is a powerful technique in engaging students and differentiating work for them. Some students found just calculating the volume of each box was challenging enough. Others found it simple, and it was their own desire to avoid doing the ‘boring’ calculations that drove them to using different mathematical techniques to find the solution faster. In this case, generalising the problem by describing it algebraically required deeper thinking.
The use of Desmos forces them to represent their with appropriate algebraic notation. Another solution students could have used would be using a spreadsheet. While that wouldn’t use mathematical notation, it’s still teaching them to represent abstract ideas with symbols.
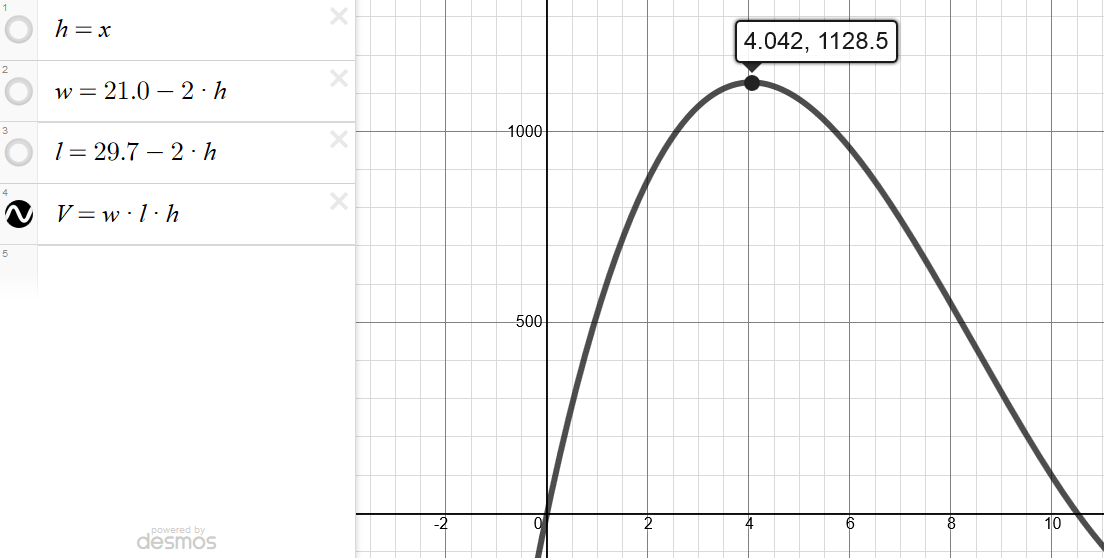
Of course, they would have been really annoyed at me had they known the solution can be found just by doing this:
Though my students didn’t get to it, I also prepared the following extension question: