This is the second skill for Algebra 2, which is pretty much what it says in the title.
At this point, we’re almost ready to start talking about functions, but I wanted to “review” a few things about solving equations first. Which brings us to these pages.
Except, lets just pause for a moment, and examine those quotation marks around “review”. The linear equation stuff is straight-up review, but solving absolute value equations is one of those used-to-be-in-2-but-now-in-1 topics I wrote about last time. Which means it’s new to my students this year, but should be something my future Algebra 2 students have already seen. With that out of the way…
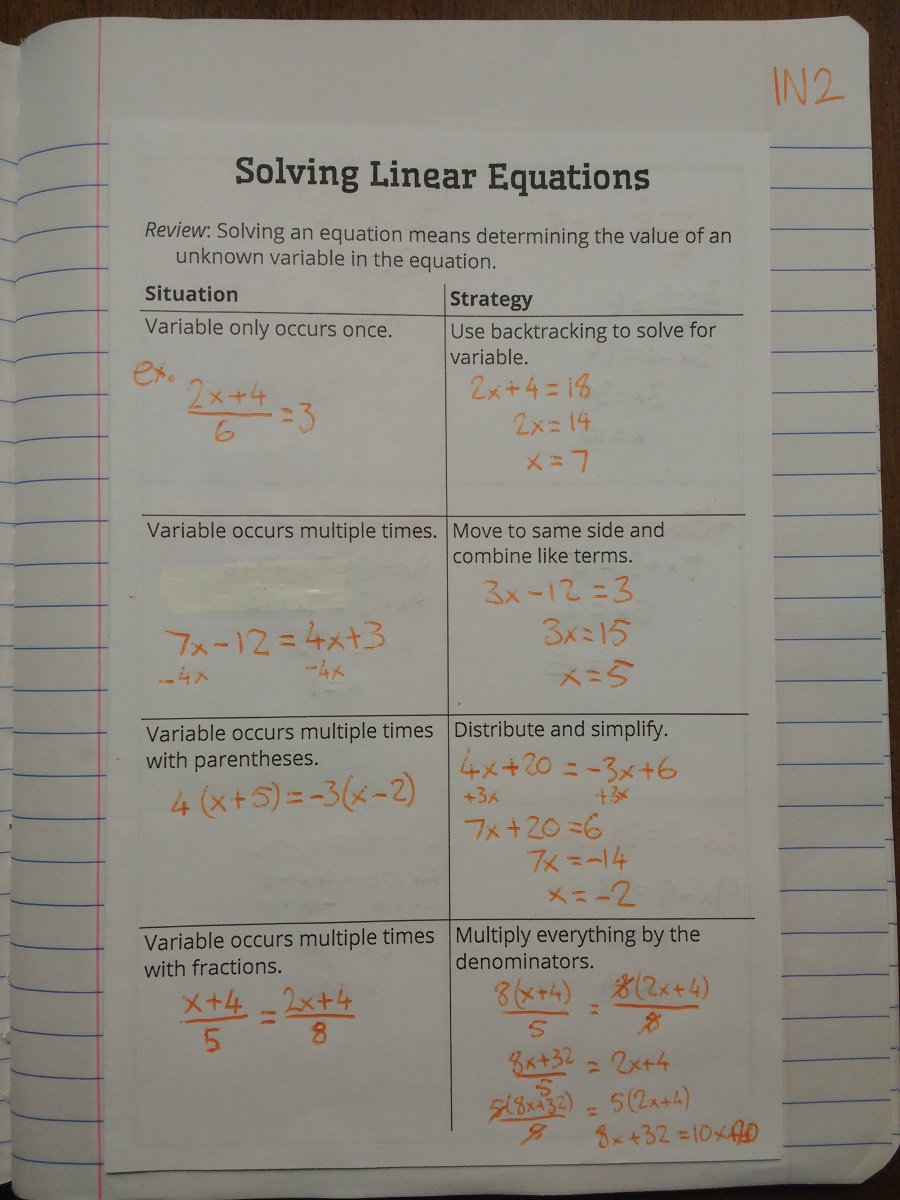
Nothing terribly complicated here. These should be equations my students know how to solve, but as I suspected would be the case, they needed some help shaking some of the cobwebs loose first.
I find students get a lot more frightened of linear equations than they need to be, especially when fractions start showing up. This was a good chance to have them use a strategy that shows up again and again in algebra:
If you don’t know how to solve this problem, turn it into one you can solve.
And that’s the principle behind the design of these notes. Each situation shown really only requires one or two steps to turn it into an equation like the one above.
I would never suggest teaching this stuff for the first time like this. There needs to be much more time spent developing understanding at each stage. But for review, I think it worked fine.
I very purposely didn’t use “cross-multiplying” as the final strategy. Those words are banned in my classroom. While it could solve the example shown, cross-multiplying is useless for any problem involving more than two fractions, for instance. Every so often, I have a student suggest cross-multiplying as a way to solve a problem. Never have any of them been able to apply it the way they were supposed to. So, I’d rather my students take one more step to solve an equation and actually understand what is happening, rather than totally confuse themselves.

Absolute value equations are not in the Algebra 2 standards, but I wanted to include them anyway, because:
- These students missed them in Algebra 1. (Which means I’m supposed to cover them anyway.)
- AFAIK they’re on the ACT. They’d be some pretty easy points my kids would be throwing away if they didn’t know this.
- I’m about to use absolute value functions as an example for transformations and graphing, to set up everything we’re going to do with other functions. It’s probably a good idea if they knew how to find some x-intercepts, then.
- I think it’s going to be useful to expose students to equations that can have two, one or no solutions. I heard a rumor that there’re these things called quadratics that do something similar…
- I also wanted kids to practice finding extraneous solutions, because that’s going to come up soon, too.
Notice that the notes don’t point out that the absolute value function cannot equal a negative number. That was there originally, but I took it out, and let students solve a few equations first before we talked about it. I was hoping they’d realize themselves, but it did take a little bit of prompting for them to realize that something like |x – 2| = -3 has no solution without having to go through all the steps. In any case, it show the value of checking the solutions of an equation.
In case you were wondering, it is possible to get an absolute value equation that has one legitimate solution and one extraneous solution. Try something like |x – 2| = 2x.