So after my last post I started to have a crisis of confidence in what I was planning to do. I felt like I oversold my plans a bit too much. What if this is a complete disaster? I’ve kind of committed to blogging about it now!
Thankfully it seemed to go well, and the feedback I got from the students was really positive.
So anyway, introducing…
(drum roll, drawing out the tension, not really a surprise since it’s in the title…)

So this is the idea – Thursdays are now all about ‘new things’. As I wrote last time, I want to capture the excitement of discovery that I see in maths but seems to go unnoticed by students. By putting the idea that this is something new front and center, I’m hoping I can sidestep that part of a kid’s brain that tells them each lesson is just the same old boring maths.
So I’m putting these rules on myself for Thursdays. That said, I’m completely prepared to break these rules I feel the need to. And given that New Things Thursday is itself a new thing, it may need to change.
Rules for New Things Thursday
-
Each lesson will be about on something new. A new rule, a new concept, a new perspective, whatever. We will still do some revision, and the new content will build on what the students already know, but the ‘new thing’ will be the focus of the lesson.
-
Rather than explicitly telling students the new thing, I will find a way to let them discover it themselves. This will be a challenge, as it will take a lot longer to introduce each idea, but hopefully it leads to more solid understanding from the start.
-
For each ‘new thing’, students will create a ‘new thing page’: a page in their workbooks that summarises the new content. This page will be their main reference to the concept in future lessons.
To set the tone of New Things Thursday, I’m also allowing students a few minutes where they can share with me and the class any ‘new things’ that they’re excited about, which can be whatever they’re interested in and doesn’t even need to relate to maths. (I realised afterwards that I may have subconciously ripped this idea off from Sarah Hagan’s Good Things Mondays, so thanks goes her. Actually, most of elements of New Things Thursday are probably stolen from other bloggers.)
The first New Thing: Pythagoras’ Theorem
Introducing Pythagoras is always an interesting moment; it’s one of those key points where high school maths transitions from being ‘arithmetic’ to ‘mathematics’, and might even be the first time students hear the word ‘theorem’.
The statement of rule (a2 + b2 = c2) is so simple to students that they don’t always recognise the significance of it, and unfortunately it is often only treated as a tool for calculating lengths. I think our aim should be to helps students realise the surprising elegance of the theorem, the mathematical truth it reveals.
We started the lesson talking about square numbers and I asked why they were called ‘square’ numbers. It took a little prompting, but they realised that they relate to the area of squares. I had them list all of them from 12 to 202, which didn’t take too long. Once they had their lists, I pointed out that 144 + 25 = 169, or 122 + 52 = 132.
I asked if they could find any more combinations like it, and gave them a few minutes in groups to see how many they could find. (I deliberately didn’t use 32 + 42 = 52 as my example so they would have an easier one to find.) A few students asked me whether the ones they’d found were correct. I told them they didn’t need to check with me – they could check themselves using their calculator.
I then listed the combinations on the whiteboard. Some had found up to 82 + 152 = 172. Some had realised that many were multiples of 32 + 42 = 52. (YES!) I had each student choose one equation from the board, and asked them to cut out three squares representing the numbers in their equation from grid paper that I had handed out.
Notice that so far I have not mentioned triangles or right-angles, or even the name Pythagoras. That was the secret truth that I wanted my students to discover.
I asked them to create a triangle by using the edges of their squares. What sort of triangle was it? It turned out they all had right angle triangles!
It was at this point that I finally put up some notes about Pythagoras’ theorem, and had them create their new things page. I’d already prepared one myself in case any students didn’t know what to put on theirs:
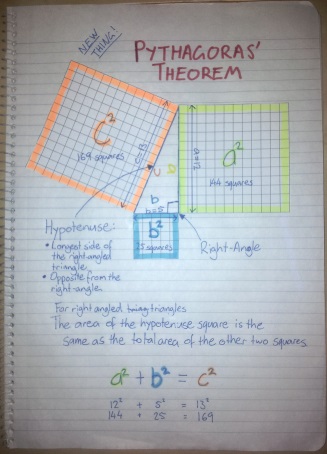
Thankfully a lot of of the pages the class made looked a lot better than mine. Some students even decided to create a ‘new things’ section in their book so it would be easier to look up in the future.
I pointed out that though we’d discovered this pattern, it’s not really a theorem until we prove it – which hopefully will happen next lesson.
Unfortunately, that was the last Thursday I’ll have them this term – they have an excursion next week and I have one the week after. But I think I’ve built some enthusiasm from the class for ‘new things’, and set a pattern we can start in earnest next term. And anyway, there’s no reason I can’t do this:
