Category: Uncategorized

To start by stating the obvious: I have not blogged enough this year. As in, my last post was before the school year had even started. I could make excuses (which would basically consist of ‘way too busy’, ‘not enough time’, ‘seriously, I’m crazy busy’), but I know I’m a better teacher when I blog. I know the constant process of self reflection is good for my ability to be self-critical.

Now that I’m starting my favourite topic of all time with Year 7, Primes and Indices, I thought this was a good chance to get back into this blogging thing. As my girlfriend reminded me the other day, I’ve been known to write ‘#primenumbersaremyjam’ in messages before. Number Theory was my favourite uni subject by far. And, I guess you noticed the title of this blog. I also may have gone through the proof that there are an infinite number of primes with my Year 12s today (which has very little to do with the differentiation we were supposed to be doing).

So I get just a little bit excited when I get to teach this. 😉

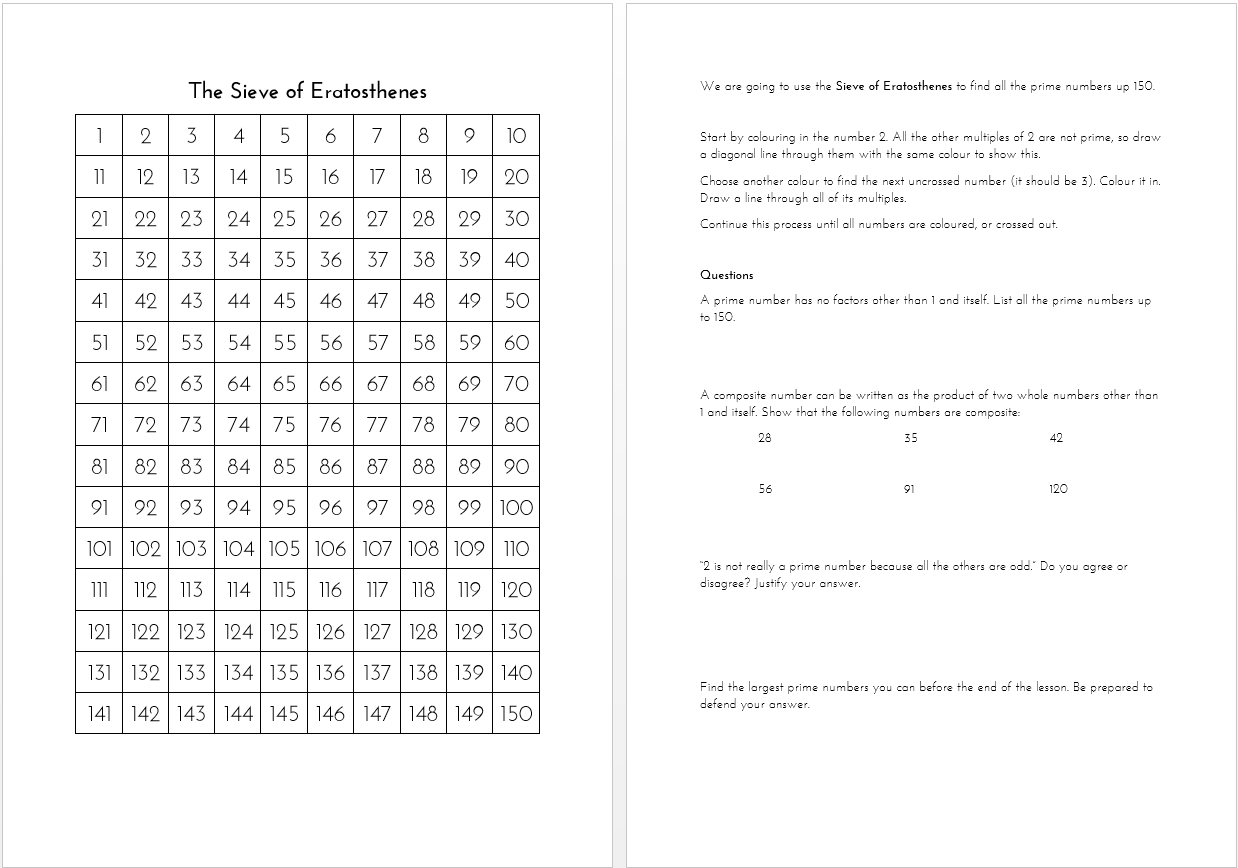
So, the Sieve of Eratosthenes, aka ‘that thing where you cross off a bunch of numbers to find the prime numbers’. If you’re not familiar with it, the process is this:

• Ignore 1, because it is neither prime or composite. 🙂
• Select the first number, which is of course 2. We’ve found our first prime!
• Eliminate all the multiples of 2 (except 2 itself), as these are not prime.
• Select the next number that is left, which should be 3. This is also prime.
• Eliminate all the multiples of 3.
• Select the next prime number, which is 5. (4 was eliminated by 2). Eliminate its multiples.
• Continue this process to find the rest of the prime numbers.

I googled for a worksheet for this (or really any number grid would’ve done), but I wasn’t really happy with what I found. Most number grids seem to go up to 100 or 120, but I wanted to go to 150. Mostly so I could include 121, and make it necessary to cross off the multiples of 11 (there are smaller multiples of 11, of course, but they’re all eliminated by the smaller primes). The next step, then, was to throw together my own worksheet, which looks a little (or exactly) like this:

Some people may have decided that ‘Finding Prime Numbers’ would make a better, less confusing title for students, but I disagree. I think we need to expose our kids to the accepted terminology, so they can communicate in correct mathematical language. We just need to teach them what the terms mean, which is our job, by the way. I get rather annoyed when I see students being told they’re studying ‘chance’, say. Call it ‘probability’. Because that’s what it’s called. #pettyrantover

I decided that this time I would be really precise with how I wanted students to mark off their sheet:

• Colour in each prime completely using a different colour. (After 11, I let them start using a single colour, because they would have run out.)
• When eliminating composites, draw a single line through each multiple in the same colour as the prime number. If a number has multiple prime factors, it gets multiple lines through it.

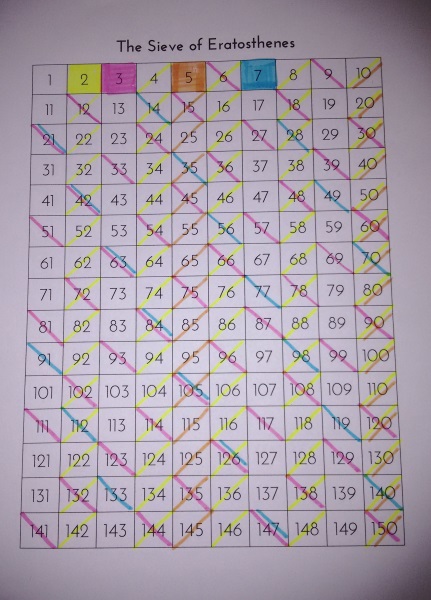
My partially completed sheet. Unfortunately the rest of my awesome highlighters are at school, and I am at home. But it should give you the idea.

This, for one thing, made the sheets a lot neater. But it also made it easier for kids to notice patterns. Patterns which they kept showing me completely un-prompted. I had students not only tell me that the multiples of 11 make a diagonal line, but they explained why that happens. #mathsteacherjoy

Another moment of joy came when I saw students write down their reasons that 2 is prime, using the definition of prime numbers. 🙂

Downloads for this worksheet are here:

• PDF: The Sieve of Eratosthenes.pdf
• Editable Word document: The Sieve of Eratosthenes.docx
  (You’ll need the font ‘Josefin Sans’ if you don’t want it to look weird.)

Hi there! Despite possible reports to the contrary, I am still alive. Yeah, I know it’s been a very long time since my last post. It’s not that I haven’t had anything to write about. Things have been very busy for me. But that’s really just making excuses.

So new year means new school year (which always seems to surprise northern hemisphere readers), which means a whole heap of changes. Here are some of the things I have to look forward to this year:

New classes

My maths class this year are

• Year 7 Maths
• Year 9 “Exploration”
• Year 10 Maths (in Semester 2)
• VCE Maths Methods Unit 3 & 4

as well as IT classes

• Year 9 & 10 Software
• VCE Information Technology Unit 1 & 2

(I’m probably just a little bit too excited about not having to teach physics this year!)

These are mostly subjects that I’ve taught before (if a few years ago), but I’m excited to see how I’ll be able to refresh the way I teach each of these. The exception is…

New subject

… Year 9 & 10 Software. This isn’t just a new subject for me. This is a new subject for the school which I basically invented, am currently developing and will teach for the first time this year. Okay, claiming I “invented” the teaching of programming is going way too far, but it was my idea to make it an elective at our school. This is part of an ongoing effort to refresh our ICT offerings, which also involved me teaching “Web Development” last year.

There will be a lot of experimentation as I figure out the best way to deliver this. We will be using Python as our language, but there are many different things we could actually end up doing with it.

The nice thing is that I’ll be able to teach whatever I want (within reason), which means sneaking a lot of maths into the course. 😉

New classroom stuff

I’m tweaking the way I do a lot of things in the classroom, including my marking, quizzing, classroom rules, notetaking, and more. It’ll be interesting to see how these go. Hopefully I’ll elaborate more in the future.

New Old responsibilities

My non-teaching responsibilities are mostly the same as I had last year, but I’m hoping that the year of experience will allow me to consolidate and build on those roles this year. In particular, I’m hoping we make significant progress on examining and improving our sequence of maths pedagogy throughout the entire school.

New blog posts!

Yay! Hopefully a bit more regularly! (I can dream, can’t I?)

New, um, personal stuff

The last part of 2014 and my summer holidays were, for lack of a better word, amazing. I’m not going to go into any of that now, but hopefully (if you care) I’ll get around to sharing more information eventually. Let’s just say that I while I hoped that getting involved in the MTBoS would affect my professional life, I never knew it would change the rest of my life quite this much. If you really have no idea what I’m talking about, there are clues on twitter and in other blogs. 😉

*EDIT (2015-08-12): So, that got a bit cryptic at the end. 😉 If you really want to know what I was talking about, you might want to read this.

So Year 12 are gone and finished their exams a few weeks ago. I always feel a little sad saying goodbye to my Maths Methods students. I have so much fun with them and get to know them pretty well over the year, and this year was no exception. One thing that was different was the fact that I lost the competition we have over the year. Well, if I really wanted to I could claim the win on a few technicalities (drawing on my posters on muck-up day should’ve cost them a few points), but I’ll let it slide.

They decided that if they won, their prize would be getting to write a blog post for me, so this is it. I’m trying to resist the urge to clarify and explain a lot of their comments. Just be aware that some of the things they say might not be 100% accurate… 😉

Next year is not looking good. I’m already down 4-0 after one week of headstart classes…

Mr Carter’s assessment report

Stop

• Looking for your favourite class, you found them this year.
• Giving yourself points for no reason.
• Whinging about hockey injuries, only to find out they don’t exist.
• Giving yourself eighteen points in a lesson as a final attempt to regain dignity in the class competition, no one likes a bad sport.
• Forgetting to bring your laptop charger to class, those minutes of absence, added up might have changed our scores by one or two marks, changing our ATARs, changing the outcome of our future.

Start

• Being fair when awarding points, it’s not “discouraging class participation”, it’s playing strategically.
• Telling students when you are going to be away.
• Preparing students for exams in term one, then they might have a chance.
• Removing sections from the textbook from your study list, particularly: algebraic techniques, functions and graphs, transformations, algebra of functions, differentiation and anti-differentiation, graphs and modelling, discrete and continuous random variables, and the normal distribution. So basically everything.

Keep

• Encouraging students to do maths, but not specialist, that’s just silly.
• Teaching methods so that students don’t have to suffer through distance education.
• Diverging from the maths question you were asked to interesting topics, so that despite students not doing any textbook questions for the lesson, they continue to learn.
• Telling (rubbish) maths jokes, they’re not funny, but at least you tried.
• Telling us how methods can be used in real life, it gave us some hope that the 146 hours we spent in that room this year will be worth it.

Change

• Your lesson plan so there is cake every Wednesday, and so we don’t have a double on Friday afternoon.
• The way you spell chai in the methods probability SAC, it’s not spelt chi.
• The computer for which the license agreement for the CAS software is on, we feel that the five seconds that it takes for you to click on the ‘continue free trial’ button is a major disruption.
• Your career guidance strategies, you’ve successfully convinced us to never become a maths teacher.

Even after all our comments, you are, and always will be our favourite 3/4 maths methods teacher that we ever had, just as we were your favourite methods class. Deep down we did sort of like methods, we just wanted to take this opportunity to whinge about is this one last time, and at least it was better than English (in our reality). So thank you, Mr. Carter, for being our final maths teacher, and for making methods as enjoyable as you could.

Second last week of the year, and my Year Nines have a serious case of the I-don’t-cares. End-of-year activities next week and the fact their reports were written last week have given them the idea that they don’t really need to work this week.

Unfortunately for them, I see this as one last chance to do maths with them this year. So we’re doing maths. The good news is my love of Desmos is starting to rub off on them, so they were happier about working when I told them we were using it.

On Monday we looked at the y = a (x – h)² + k form of quadratic functions, and how to produce its graph by transforming y = x². I could have done this by telling them what each of the transformations were, then have them repeatedly sketch graphs. Instead, I wanted them to actually investigate how to produce the transformations themselves.

I gave the students the following sheet of instructions:

This was written in a bit of a rush, which explains the mistakes (well, that’s my excuse, anyway). In Set Three, I’ve included y = x² twice. When the kids called me out on that, I suggested they make up their own function that they think fits the pattern in the rest of the set. Even though this wasn’t my original plan, I’m thinking now that having students add their own examples to each set might be a good idea.

And Part 2 was just badly written. I found I had to re-explain it numerous times over the lesson. I’m okay with my students being confused because they don’t know how to do something, if it leads to them thinking for themselves to figure a problem out. But it’s not okay that they were confused about what they were being asked to do. (Note to future Shaun: your question is broken, FIX IT before you use it again!) If it’s not clear, the intention was to create something like this:

Part 3 was shown on the IWB rather than on the handout:

Using what they created in Desmos, they needed to find the equation that matched the parabola described. This worked really well – it made students think about how changing the equation transformed the graph. At no point did I tell them that (h, k) is the turning point, or that the y-intercept could be changed by dilating the graph. They had to work this out for themselves. And when they thought they found the equation (and inevitably asked me if they were right), I could tell them to type it into Desmos themselves to make sure it worked as they expected.

The last one worked well, because the students found it much harder than the others – leading to a great discussion about why this form of the equation is not so useful in that situation. Given we just covered the null factor law last week, we were able to discuss how the factorised form was more useful.

Unfortunately, this is as far as we got. My kids can feel the end of the year coming, so they don’t think they need to work. In an ideal world where I didn’t have to stop students from online shopping and playing games instead of opening Desmos, I would’ve continued a bit further with the lesson:

• I wanted students who finished earlier to create their own questions for Part 3, and add them to the list for others to do (which is why this part was on the IWB).
• One nice thing from this lesson was that students were exploring dilations, reflections and translations without me telling them what they are. But that does mean they still don’t know those terms. I wanted to finish the lesson by taking a few notes to define the terminology.

It was more than a little frustrating to not be able to finish this off properly. But I think the work we did get done worked well.

So I ended my last post with the words “I’m excited to see where we end up on Monday”. And now it’s been a month since I actually taught that lesson, and I haven’t blogged since then. Oops. Let’s see how I go remembering what we did…

Quick recap (though I really suggest you read that last post): we were trying to determine the optimum position to kick a rugby ball from to maximise the angle towards the goal the kicker has to aim for. Students worked in groups to figure out a method to calculate the angle, and tried various distances to see what angle resulted.

Diagram I drew on the board at one point, showing some of the angles we were calculating.

The method that each group eventually used was to calculate the angles in the two right-angled triangles, then subtracted the small one from the big one to get our kicking angle.

Students had calculated angles for a few distances by hand, but this was going to be a slow process. So, I suggested they use their computers instead to do the boring manual work. I didn’t specify what software they should use, though I did give them some hints.

The awesome thing about this was that it forced them to think about about the problem abstractly. To get the computer to do the work, they needed to specify how to get the solution generally. So, here we are in a trigonometry unit, and students are inventing and using variables themselves to help solve their problem.

Some groups used Excel:

and others used Desmos:

One group was using Geogebra too, but I didn’t get an image of that.

Each group basically used trial and error, but got the various software to do the calculations for them. I loved the way this showed students the power of thinking algebraically. By using variables, they could generalise the problem. Desmos makes this use of variables explicit. But even using Excel, where there are “Cell References” instead of “Variables”, the same kind of abstract thinking is needed.

As this was a Year Nine class, we didn’t go beyond using trial and error. But afterwards I did play around in Desmos for how you might approach it in a class involving calculus:

In this case, “b” is the distance from the goalpost to where the try was scored, and “x” is the distance from the try line where the ball is kicked.

My major take-away from this lesson: the use of technology should always support getting students to think deeper about problems. Get them to think abstractly. When the boring manual work is removed by the appropriate use of technology, students are freed to experiment, to change the way they approach problems without the cost of losing a large chunk of lesson time to busy work.

What I’ve been doing lately

So, there are a few reasons why I haven’t posted anything for a month. My non-classroom responsibilities have seen me busy with VCE exams, preparing students subject choices for next year, and a few days out of school at various trainings and meetings. Also, my life outside of school suddenly got very busy as well. Don’t worry, everything’s good, but time to blog seems to be less available than it once was. But I’m hoping that as the year starts to wind up, I’ll be finding more free time to clear out my backlog of blog post ideas 🙂