Category: Uncategorized

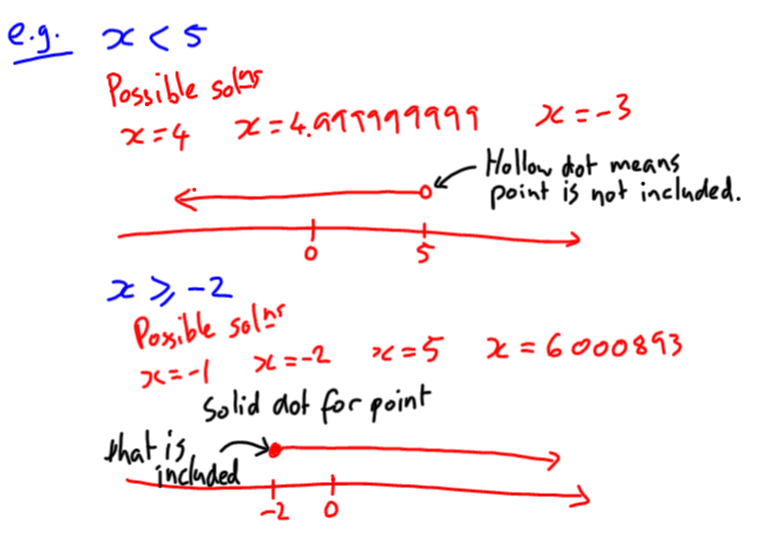
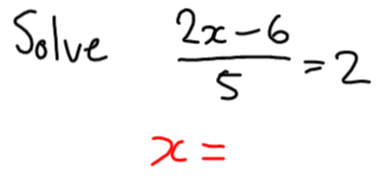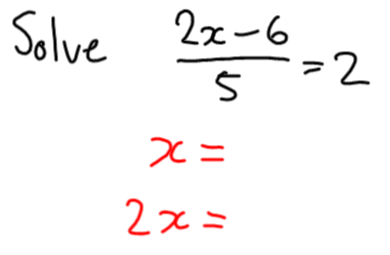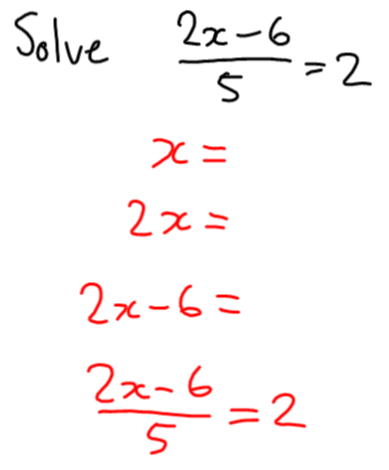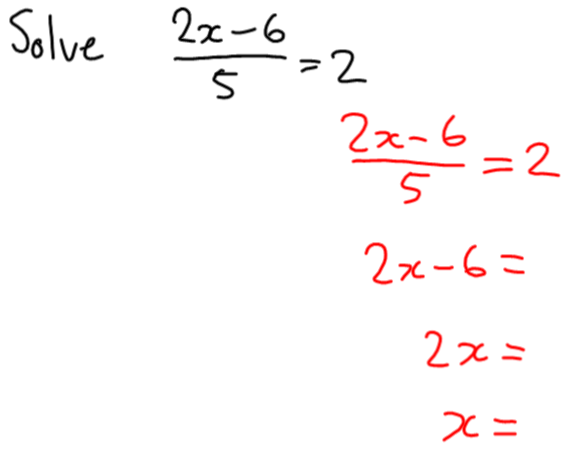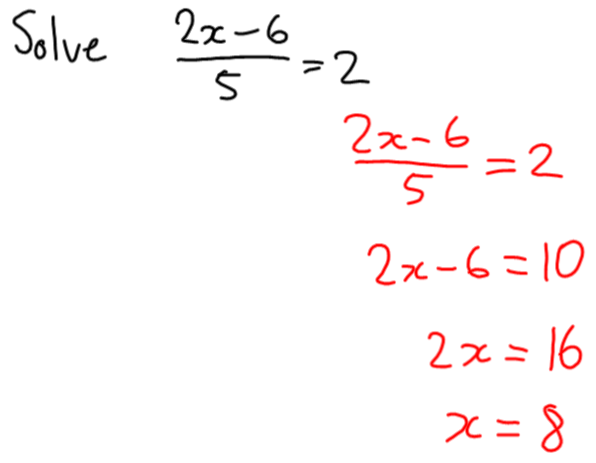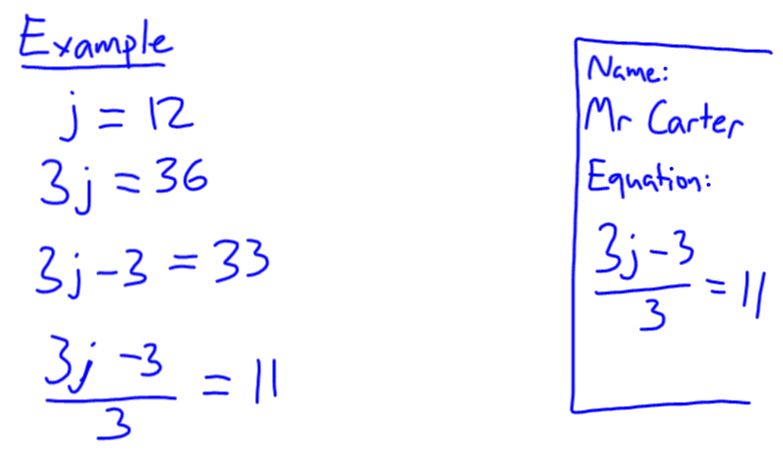To be clear, this is the strangest post I’m ever going to write. Completely unlike any other you’ll see on this blog. This is about what’s been happening in my life personally. But also totally about teaching math. And blogging. And the MTBoS. And the fact that I dropped the ‘s’ off the word maths just now.

This kangaroo is also related to the story. Sort of.

I’m not exactly sure how to explain what I’m about to share. I’ve been thinking about this for a while, but haven’t really gotten anywhere. But I promise what I’m about to share is totally worth hanging around to read.

Last year I started dating this really amazing girl. Someone who really inspires me. She is so wonderfully talented and passionate about what she does. She is so incredibly cute. A couple of months ago, I got down on one knee and asked this girl to marry me. And with a single word, she made me the happiest guy in the world.

(That word was ‘Yes!’, if that wasn’t immediately obvious.)

Now, if I just left this post here, that would be exciting enough. It’s certainly the most exciting thing that’s ever happened to me. But there’s a twist to this story. Because if you’re the type of person to read my blog (i.e. a mathematics teacher who reads mathematics teaching blogs), there’s a good chance you’re already familiar with this person.

My fiancée is Sarah Hagan, who writes Math = Love.

Yeah, that really happened. I really started dating a girl who lives on the other side of the world to me. I really fell in love with another math teacher who goes by the name @mathequalslove. I feel like I need to apologise to everyone who wanted to catch up with Sarah at TMC15, because she spent her summer in Australia with me.

If this seems like a story that’s too ridiculous to be true, it seems like that to us, too. But here we are. I discovered the MTBoS at some point in the first half of last year, and Sarah quickly became one of my favourite bloggers. One day I left a comment on Sarah’s blog, not realising that by doing so I’d caught her attention as well. Over time, the messages between us increased, and we discovered that we have a lot in common, even aside from being teachers who blog about mathematics. Eventually, our messages led to us talking over Skype, when we finally realised we were both really into each other.

If you want to read Sarah’s take on this same story, click on through to find that. Though given her blog’s popularity, I’m guessing most people reading this have already seen it. 🙂

The other day I wrote a post about having students build their own equations. I decided to use this idea as a starting point for solving equations by backtracking.

The class has already solved equations in a number of ways, and even used flow charts to solve them with backtracking. But now I’m trying to introduce them to more formal algebraic notation to show their backtracking. As it turns out, they’ve already written their working out like this before, last lesson. Now they need to learn to write each step working backwards.

I wrote the following on the interactive whiteboard:

I made it clear that I was making this equation up as I went, and that I was following the exact same process as they did when they constructed their own equations. The only difference being that I haven’t written down all the steps for them to see.

Their job is to figure out what those steps were.

I asked them what I would’ve done first. “Chosen x as a variable, and a value.”

Of course, we don’t know what that value is yet. But we can work out what operations I did to it. So what did I do first? “Timesed the x by 2.” One of these days they’ll learn to say “multiplied” instead of “timesed”.

Then, it was subtract 6, then divide by 5. And, of course, our final result was 2.

Now, we need to work backwards through these steps. Here’s the cool bit, and the advantage of using an IWB for this lesson: I can drag the steps around and reorder them:

So in the last step, I divided by 5 and got 2. What number did I divide by 5?

And what number did I subtract 6 from to get 10? What number did I multiply by 2 to get 16?

And now we have our solution. 🙂

Now, I’m not expecting students to write these steps out forwards, just to write them out again to do them backwards. But I’m hoping that seeing this highlights for students that these steps of working that we write down are not arbitrary, but actually result from somewhere.

I can imagine using blank cards as a way to have students write down the steps, then reorder them themselves. Unfortunately, this was an idea I only had part way through the lesson.

Unsurprisingly, the expectation that students should show each step of working (and particularly my warning that I would mark any quiz questions missing working as wrong) annoyed some of them, particularly the stronger students. “Why should we show our working if we already know the answer.” Of course, I don’t particularly care that their answer is correct if they can’t convince me that their answer is correct.

Year 7 are currently working on solving equations with pronumerals for the first time. Specifically, we’re using backtracking to solve multi-step linear equations.

This year, I realised there’s a problem with getting students to understand backtracking. Before I can expect students to work backwards through steps to solve an equation, I need to make sure they understand how the equation goes forwards. I think that in the past I’ve been too quick in jumping into backtracking, without spending time on fortracking (I know that’s not a word, but I’m running with it).

I’m at an advantage over my students when they see an equation I’ve written. I’ve seen the entire process. I started with a variable and its value, then I applied a number of steps to build it into an equation. Then I know that the solution can be found by working backwards through those steps.

But students only see the last part of that process. And while a few students can look at that equation and see the steps hidden in it, many have no idea where the equation comes from or what it represents. My solution: pull back the curtain, and let students see the entire process themselves.

I created this worksheet for “building equations”:

After I gave and example, each student create five equations. Then, they wrote the final equation and their name in one of these boxes along the bottom of the page:

Then each student gave their equations to other students, who then glued them in their workbooks. The plan was for those students to solve these equations, but this had to be left to a later lesson, as the “building” part of the task took longer than I expected.

This was okay, as it allowed me do identify weaknesses a number of students had, particularly with the order of operations. One student ended up with 3(x + 1) in their equation, despite wanting to do the multiplication by 3 first. It seems they realise that parentheses have a role in deciding order, but are confused about how they work.

I started the activity by getting the class to talk me through an example, which students copied onto their sheets:

[An aside for me to remember later: Some of my kids seem to be amused by problems that involve using the same number repeatedly, hence all the threes. But in copying it here just now, I realised that (3j – 3)/3 is, of course, just j – 1. But also, (nx – n)/n is also x – 1 for any n. I wonder if there’s some activity I can create that involves exploring that fact?]

If you want a copy of this worksheet, you can find it here:

• Word document: Building equations.docx
• PDF: Building equations.pdf

Semester 2 has started, which means the Computer Science elective I was teaching has ended. The good news is, I’ve taken over Year 10 Maths, which means my teaching load is more maths than it’s ever been before. I haven’t taught Year 10 for a couple of years now, and I’ve changed the way I teach a lot even in the last 12 months. Luckily, I had this same class last year so they’re pretty used to how I do things.

The first unit I’m teaching is Linear Relationships:

Most recently we’ve been working on LR2, linear inequalities. If these are taught as a totally procedural matter, it’s a fairly easy topic: solve them the same way as equations, just being careful with the direction of <, >, ≤ or ≥ if dealing with negatives. But as I always tell my students, I believe our aim is not to ‘get the right answer’, but to understand.

In particular, I want my students to understand that there is not just a single solution, but a whole set of solutions. I want them to understand that when we write a statement such as x ≥ -2, we are describing a rule by which some values are included and some are not. So I started the lesson by looking at a couple of examples:

A little is lost when seeing this as a static IWB page, as opposed to the notes that developed through class discussion. Importantly, all the possible solutions were provided by students. I was really pleased with their suggestions, in that they illustrated some important points about inequalities. For example, 4.999999999 is indeed less than five, as are all negative numbers. And I liked the suggestion of 6000893, pointing out that there isn’t an upper limit for x ≥ -2. And I impressed the student by hearing and remembering the number he called out :).

Next I gave an example of an inequality to solve. Rather than getting the class to solve it as an equation, I had them each make a list of five values that would be included in the solution, and five that are not. We then shared some of these as a class:

What this allowed us to do was find the solution to the equation by understanding what the equation described. It’s important as a maths teacher to ensure students know why they do things they do. When students solve equations, they shouldn’t following a list a pre-described steps to get ‘the answer’. They should be trying to answer the question, “What value makes this statement true?”

We also looked at 23 – 2x ≥ 15, and found that our solution doesn’t necessarily have the same direction as the inequality. My students quickly identified the negative in front of the x as the culprit. As one student pointed out, you need to make x smaller if you want 23 – 2x to get larger.

So, the class found two important pieces of information are needed to find the solution to an inequality:

1. What is the boundary between the solutions that are included and the solutions that are not?
2. Which direction do those solutions go in?

And how do we find this information? Using algebra, of course!

It’s at this point that I believe procedure becomes useful: after that understanding has been built. I’m increasingly finding that a good way to get students to follow a process I give them is to use a less efficient method they understand to do the same thing first. Students could solve inequalities by finding test cases each time, but they find solving them algebraically is a much quicker process. They look for shortcuts to make their work easier. Just like mathematicians do.

Firstly, credit where it is due: I was given this idea by Sarah Hagan, who found it on Annie Forest’s blog. So, thanks!

So, Petals Around the Rose (the name is really important!) is a game/puzzle which, if you followed that link just now, is likely making you really frustrated (sorry about that). Five dice are rolled, and you have to predict what score those dice make (and I promise that there is logic to how the computer decides the scores). If you use the site I linked to, you enter your prediction before seeing what the actual score was.

For the last couple of days, I’ve been using the puzzle in the last 5 minutes of my lessons with Year 7. One student has already seen the puzzle before (and is taking great pleasure in keeping the solution a secret), but as of yet, none of the others have figured it out.

They are trying, though. My students are very determined to find out what the answer is, and keep suggesting their own theories, unprompted. Because of how the game works, it’s easy to get them to test their theories – roll the dice again, and get them to give the score. Even if they manage to be right that time, it doesn’t take long to find a roll where their theory fails. But this is what mathematics is, right? Noticing patterns, coming up with conjectures, testing those conjectures, and going back to the drawing board if it doesn’t hold up.

This is their score as it stands now:

I’m not sure how we’ll proceed with this now. I might wait until next week to bring this out again, but I do want to keep playing the game with the class until they figure it out. We’ll see how long that takes.

The question I’ve been leading to is this: How do I get students to display this same determination and persistence to finding actual mathematical patterns and theorems? I guess this is what every maths teacher spends their entire career trying to answer.