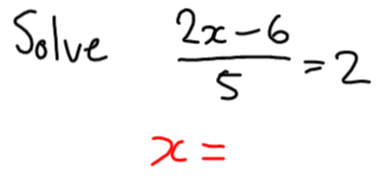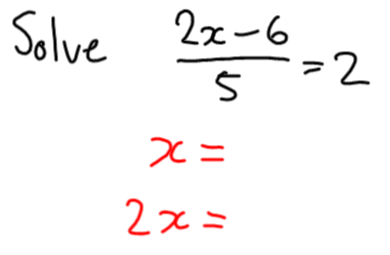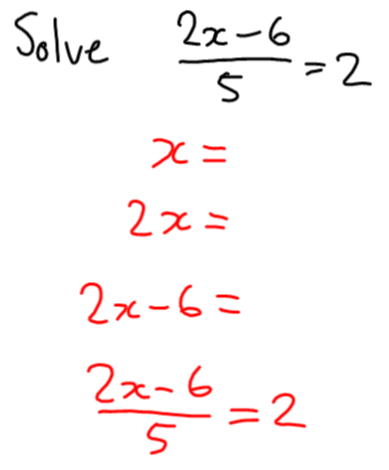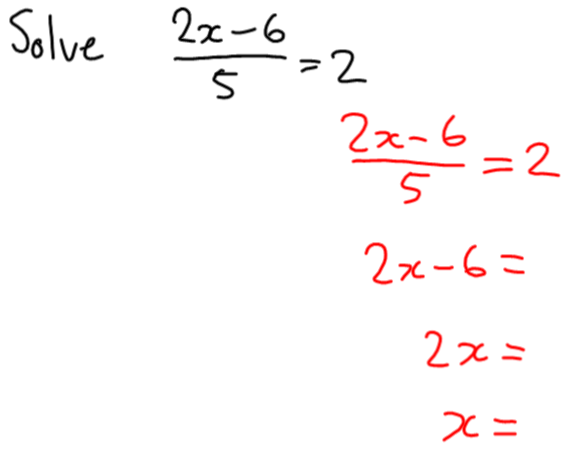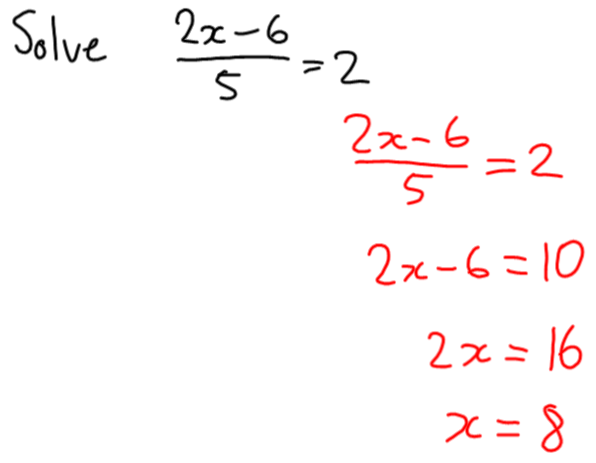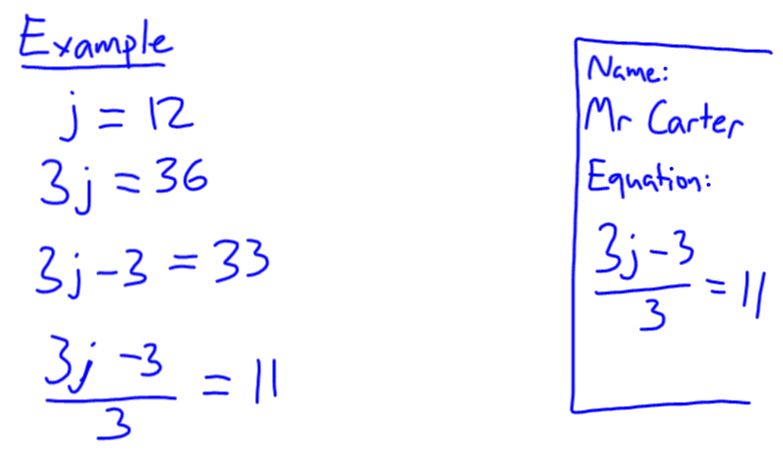Month: August 2015

The other day I wrote a post about having students build their own equations. I decided to use this idea as a starting point for solving equations by backtracking.

The class has already solved equations in a number of ways, and even used flow charts to solve them with backtracking. But now I’m trying to introduce them to more formal algebraic notation to show their backtracking. As it turns out, they’ve already written their working out like this before, last lesson. Now they need to learn to write each step working backwards.

I wrote the following on the interactive whiteboard:

I made it clear that I was making this equation up as I went, and that I was following the exact same process as they did when they constructed their own equations. The only difference being that I haven’t written down all the steps for them to see.

Their job is to figure out what those steps were.

I asked them what I would’ve done first. “Chosen x as a variable, and a value.”

Of course, we don’t know what that value is yet. But we can work out what operations I did to it. So what did I do first? “Timesed the x by 2.” One of these days they’ll learn to say “multiplied” instead of “timesed”.

Then, it was subtract 6, then divide by 5. And, of course, our final result was 2.

Now, we need to work backwards through these steps. Here’s the cool bit, and the advantage of using an IWB for this lesson: I can drag the steps around and reorder them:

So in the last step, I divided by 5 and got 2. What number did I divide by 5?

And what number did I subtract 6 from to get 10? What number did I multiply by 2 to get 16?

And now we have our solution. 🙂

Now, I’m not expecting students to write these steps out forwards, just to write them out again to do them backwards. But I’m hoping that seeing this highlights for students that these steps of working that we write down are not arbitrary, but actually result from somewhere.

I can imagine using blank cards as a way to have students write down the steps, then reorder them themselves. Unfortunately, this was an idea I only had part way through the lesson.

Unsurprisingly, the expectation that students should show each step of working (and particularly my warning that I would mark any quiz questions missing working as wrong) annoyed some of them, particularly the stronger students. “Why should we show our working if we already know the answer.” Of course, I don’t particularly care that their answer is correct if they can’t convince me that their answer is correct.

Year 7 are currently working on solving equations with pronumerals for the first time. Specifically, we’re using backtracking to solve multi-step linear equations.

This year, I realised there’s a problem with getting students to understand backtracking. Before I can expect students to work backwards through steps to solve an equation, I need to make sure they understand how the equation goes forwards. I think that in the past I’ve been too quick in jumping into backtracking, without spending time on fortracking (I know that’s not a word, but I’m running with it).

I’m at an advantage over my students when they see an equation I’ve written. I’ve seen the entire process. I started with a variable and its value, then I applied a number of steps to build it into an equation. Then I know that the solution can be found by working backwards through those steps.

But students only see the last part of that process. And while a few students can look at that equation and see the steps hidden in it, many have no idea where the equation comes from or what it represents. My solution: pull back the curtain, and let students see the entire process themselves.

I created this worksheet for “building equations”:

After I gave and example, each student create five equations. Then, they wrote the final equation and their name in one of these boxes along the bottom of the page:

Then each student gave their equations to other students, who then glued them in their workbooks. The plan was for those students to solve these equations, but this had to be left to a later lesson, as the “building” part of the task took longer than I expected.

This was okay, as it allowed me do identify weaknesses a number of students had, particularly with the order of operations. One student ended up with 3(x + 1) in their equation, despite wanting to do the multiplication by 3 first. It seems they realise that parentheses have a role in deciding order, but are confused about how they work.

I started the activity by getting the class to talk me through an example, which students copied onto their sheets:

[An aside for me to remember later: Some of my kids seem to be amused by problems that involve using the same number repeatedly, hence all the threes. But in copying it here just now, I realised that (3j – 3)/3 is, of course, just j – 1. But also, (nx – n)/n is also x – 1 for any n. I wonder if there’s some activity I can create that involves exploring that fact?]

If you want a copy of this worksheet, you can find it here:

• Word document: Building equations.docx
• PDF: Building equations.pdf