Month: October 2014

So I need to start this post with an admission: I got this activity from our textbooks. In my own defense, I really only took the initial idea from the book, but then made up the rest of the lesson myself.

So the idea I “borrowed” today was about rugby league and using trigonometry to calculate the angles involved. In particular, trying to work out the optimal position to kick the ball from to make a conversion.

Now, quick aside for those people who know nothing about league. (Sorry to NSW and Queensland readers who are about to see me butcher this explanation. I’m from Victoria, which is an AFL state, not league.) Aim of the game is to score a “try” by crossing the ball over the goal line. If a team scores a try, they get a chance to “convert” it by kicking the ball off a kicking tee through the goals to get a few extra points.

Now here’s the bit that’s relevant to the lesson. The kicker has to place the ball in line with where try was scored, but they can move forwards or backwards wherever they want.

So the textbook basically started by asking something like “Where should the ball be placed to maximise the chance of scoring?”, then proceeded to give a whole heap of smaller questions to step the students through the task. In the process, stripping out all the interesting thinking parts of the investigation and turning it into a set of mechanical steps.

I wanted my students to develop the questions themselves, and I certainly didn’t want them to learn about rugby league by reading the boring description in the book. (Again, my Victorian students don’t really know understand rugby league at all.) So in my preparation, I searched YouTube for “rugby league conversions” and found this video. I didn’t show the entire nine minute thing, just a few of the conversion kicks.

(I also showed part of this video of dreadful conversion attempts at the end of the lesson.)

I gave the kids two minutes to talk in their groups about any questions they had after watching the video. I then asked them to share these with the class. Initially, no-one wanted to answer, but after a little bit of prompting, the floodgates opened:

Sorry for the terrible writing and English. I was trying to get these written on the board as quickly as possible!

Some of their questions were quickly answered by refering to this page showing the dimensions of the field and goals. After a bit more discussion, we set about trying to work out the best position to kick from, to maximise the goal angle to kick through.

I assigned each group a different distance from the goal post to investigate. This divided the labour really well, as within groups different students could investigate different kicking distances to collect a wider range of results.

This worked really well – around the room there were kids discussing angles and distances, drawing diagrams and setting out tables to summarise their results. Groups were discussing what they needed to do to figure out the problem. And in the midst of it all, students were using trigonometry to work out their angles.

The best thing? Beyond the initial prompt, most of this happened without my input. I did have to give help around the room at various times, but students were willing to figure it out together in their groups. They also started using trig without me telling them to!

Though in fairness, it was reasonably obvious given we’re in the middle of our trig unit…

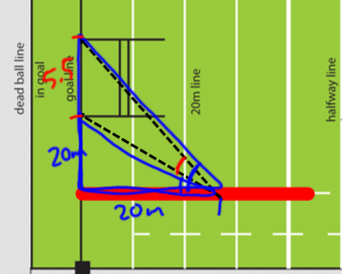
Diagram I drew on the board at one point, trying to explain… something. I’m sure it made sense at the time.

We didn’t quite get to finishing everything off, but that’s mostly because students kept posing new questions and hypotheses to investigate. A few students thought making the distance from the goal line the same as the distance of the try from the post was the best approach, and another said that 45° to the near post was best. It was great to see them slowly realise these were exactly the same thing! It was also great to see them realise their hypothesis wasn’t completely correct, and start searching for more data to figure it out.

I’m excited to see where we end up on Monday 🙂

Update: Follow up to this lesson can be found here: https://www.primefactorisation.com/blog/2014/11/26/kicking-goals-using-technology/

First day of term 4 (which was Monday – I really am running behind at the moment!) saw the start of our Trigonometry unit with Year 9. I wanted a way to get my students to start thinking about how the angles of a right-angled triangle affect its sides, while also defining the Opposite and Adjacent sides. They already all remembered the Hypotenuse from doing Pythagoras’ Theorem 🙂

So I took the class out to the front lawn and had groups of students form right-angled triangles by standing at the corners. (Actually, I didn’t say “stand at the corners” the first time, which was a good reminder that I sometimes need to be clearer with my instructions. One group tried to form the sides of the triangle by lying on the ground.) In each group, one student was given a pink sticky note to indicate they were the right angle, and another had a green sticky note with θ written on it.

Then using different colours of party streamers, the students made the sides of the triangles, defining the Opposite and Adjacent sides as we went.

As they did this, I had the groups check the other groups around them to make sure they all had right-angled triangles. This provoked great conversations amongst the groups, as they evaluated each other’s work and had to communicate clearly their reasons why a triangle was or was not right-angled.

Then I gave this challenge: make the angle at θ bigger.

As they did this, the students needed to work and talk with each other to figure out what they were going to do. Students communicating about maths to figure out a problem together! It also worked well that different groups used different solutions – some shortened the adjacent length, others lengthened the opposite – allowing us to discuss those different solutions.

Once back inside, we then worked on defining the trigonometric ratios, eventually creating this notebook page:

There was more to the lesson than that, but I’m getting sleepy now 🙂 I might elaborate on what other work we did next time.

One more thing: as we were outside, a friend of mine happened to be driving past the school. As I was talking to him that night, he asked me two questions:

• Why did I never get to go outside to do maths at school?
• Why were you making kids stand in rectangles?

I’m a little concerned about how convincing our triangles were now…